Felicidades a todos los que participaron en el final de la Universidad Politecnica de Tlaxcala, aqui les dejo la solucion de los problemas
Problema A: Palabras
En este problema solo hay que ver si una cadena se puede formar con las letras de otra cadena
# include <stdio.h>
# include <string.h>
# define MAX 1000000
char wordA[MAX + 1], wordB[MAX+1];
int hash[256];
main(){
int x;
while( scanf("%s %s", wordA, wordB) != EOF ){
memset( hash, 0, sizeof( hash ));
for( x = 0; x < strlen(wordA); x++)
hash[ wordA[x] ]++;
for( x = 0; x < strlen(wordB); x++)
hash[ wordB[x] ]--;
for( x = 0; x < 256 ; x++) if( hash[ x ] < 0 ) break;
printf("%s\n", ( x < 256) ? "NO" : "YES");
}
return 0;
}
Problema B: El señor de los anillos
Señor de los anillos, un problema que es definitivamente un dijkstra, lo complicado de este dijkstra es ver que nodos estan vistos por Sauron, como pueden ver las recurrencias son para los nodos que Sauron ve los nodos es de 1 a 7, de esa menera si sacamos el LCM de todos estos numeros tenemos esto (2*2*3*5*7) este es el modulo que necesitamos para saber si se repite sobre cualquier nodo, si nosotros ya calculamos el nodo X con el modulo Y, entonces ya no hay que evaluarlo de nuevo.
# include <stdio.h>
# include <string.h>
# define MOD (2*2*3*5*7)
# define MAX 102
int periodo[MAX+1];
int graph[MAX+1][MAX+1] , vis[MAX+1][MAX+1];
int distance[ MAX + 1 ][ MOD + 2];
main(){
int n, m, dis, node, mod, x, y, a, b, nextnode;
while( scanf("%d %d", &n, &m) != EOF && ( n || m )) {
for( x = 1; x <= n; x++) scanf("%d", &periodo[ x ]);
periodo[ 0 ] = MOD + 1;
memset( graph, 0, sizeof( graph ));
for( x = 0; x < m; x++){
scanf("%d %d", &a, &b);
graph[a][b] = graph[b][a] = 1;
}
for( x = 0; x <= n; x++) graph[x][x] = 1;
for( node = 0; node <= n; node++)
for( mod = 0; mod <= MOD; mod++){
vis[ node ][ mod ] = 0;
distance[ node ][ mod ] = (1<<30);
}
node = 0;
mod = 0;
distance[ node ][ mod ] = 0;
while( node != -1){
dis = distance[ node ][ mod ];
vis[node][ mod ] = 1;
if( node == n ) break;
for( nextnode = 0; nextnode <= n; nextnode++ ) if( graph[node][nextnode] == 1){
if( distance[nextnode][ (mod + 1 ) % MOD ] > dis + 1 && (mod + 1) % periodo[ nextnode ] != 0 ){
distance[ nextnode ][ ( mod + 1 ) % MOD ] = dis + 1;
}
}
node = -1;
dis = (1<<30);
for( x = 0; x <= n; x++)
for( y = 0; y <= MOD; y++) if(vis[x][y] == 0 && distance[x][y] < dis){
dis = distance[x][y];
node = x;
mod = y;
}
}
printf("%d\n", ( node == -1 ) ? -1 : dis );
}
return 0;
}
Problema C: Dados
Es un problema de conteo, ver de cuantas maneras distintas puedo colocar los dados para que me salga la suma solicitada, se puede hacer con un programacion dinamica o bien con un backtraking, que serviria de la misma manera, o bien cuatro fors con bastantes ifs.
# include <stdio.h>
# include <string.h>
# define MAX 5
# define MAX_CARAS 40
# define MAX_SUMA 100
int dados[MAX+1][MAX_CARAS+1];
int ndados[MAX+1];
int din[MAX+1][MAX_SUMA+1], S, n;
int solve(int position, int suma){
int res = 0, x;
if( suma > S ) return 0;
if( position == n ) return S == suma ? 1 : 0;
if( din[position][suma] != -1) return din[position][suma];
for( x = 0; x < ndados[ position ]; x++)
res += solve( position + 1, suma + dados[ position ][ x ]);
return din[position][suma] = res;
}
main(){
int x, y, prod, a , b;
while( scanf("%d %d", &n, &S) != EOF && ( n || S)){
prod = 1;
for( x = 0; x < n; x++){
scanf("%d", &ndados[ x ]);
for(y = 0; y < ndados[ x ]; y++){
scanf("%d", &dados[x][y]);
}
prod *= ndados[x];
}
memset( din, -1, sizeof( din ));
a = solve(0, 0);
b = prod;
if( a == b ) printf("1\n");
else if( a == 0 ) printf("0\n");
else printf("%d/%d\n", a , b);
}
return 0;
}
Problema D: Palíndromo
Se puede hacer con una programacion dinamica para que sea rapido o bien cuatro fors ya que el tamaño de la cadena es pequeña y saldria a tiempo.
# include <stdio.h>
# include <string.h>
# define MAX 100
int din[MAX+1][MAX+1];
char word[MAX+1];
int ispalindrome(int a, int b){
if( a >= b) return 1;
if(word[a] != word[b]) return 0;
if( din[a][b] != -1) return din[a][b];
return din[a][b] = ispalindrome( a + 1, b - 1);
}
main(){
int a, b, n, cont;
while( scanf("%s", word) != EOF ){
memset( din, -1, sizeof( din ));
n = strlen(word);
cont = 0;
for( a = 0; a < n; a++)
for( b = a; b < n; b++)
cont += ispalindrome(a, b );
printf("%d\n", cont);
}
return 0;
}
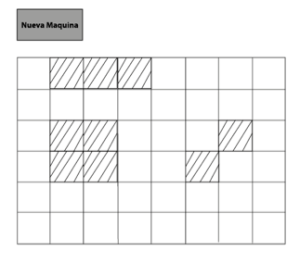
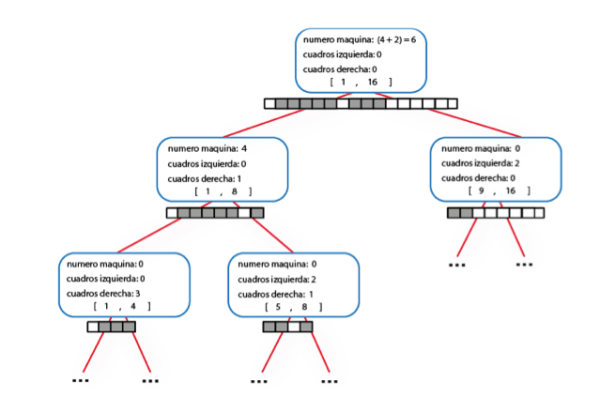
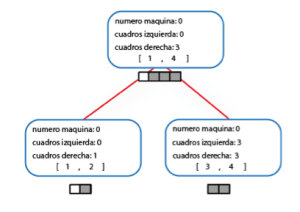
Problema E: Buscando Cuadrados
El problema de encontrar una submatrix sobre otras, en especifico sobre este problema como las matrices son pequeñas, entonces podemos hacer fuerza bruta, y con cuatro fors comparar si la matriz A esta en todas las posiciones iniciales que podamos colocarle en la matriz B, si queremos optimizarlo tendriamos que meternos un poco con el KMP, para poder hacer un conteo rapido.
# include <string.h>
# include <stdio.h>
# define MAX 100
char map[MAX+1][MAX+1], submap[MAX+1][MAX+1];
main(){
int n, size, row, col, r, c, cont, query, q;
while( scanf("%d", &n) != EOF && n ){
for( row = 0; row < n; row++) scanf("%s", map[row]);
scanf("%d", &query);
for( q = 0; q < query ; q++){
scanf("%d", &size);
cont = 0;
for( row = 0; row < size ; row++) scanf("%s", submap[row]);
for( row = 0 ; row < n; row++)
for( col = 0 ; col < n; col++){
for( r = 0; r < size && r + row < n ; r++){
for( c = 0; c < size && c + col < n ; c++)
if( map[row+r][col+c] != submap[r][c]) break;
if( c < size ) break;
}
if( r >= size ) cont++;
}
printf("%d\n", cont);
}
}
return 0;
}
Problema F: Molde!
El problema nos indica que debemos hacer un convex hull, posteriomente sacar el perimetro y el area del convex encontrado.
# include <stdio.h>
# include <string.h>
# include <math.h>
# define MAX 100000
typedef struct { int x, y; } Point;
Point Poligono[MAX+1];
Point convex[MAX+1];
int vis[MAX+1];
int n;
double valumen, perimetro;
double abso( double a ){ return a < 0.0 ? -a : a; }
long long cross_product(Point a, Point b, Point c){
return (b.x - a.x)*(c.y - a.y) - (c.x - a.x)*(b.y - a.y);
}
long long cross(Point A, Point B, Point C){
Point AB;
Point AC;
AB.x = B.x-A.x;
AB.y = B.y-A.y;
AC.x = C.x-A.x;
AC.y = C.y-A.y;
return AB.x * AC.y - AB.y * AC.x;
}
double area2D_Polygon( int n, Point* V ) {
double area = 0;
int i, j, k;
if (n < 3) return 0;
for (i=1, j=2, k=0; i<n; i++, j++, k++) {
area += V[i].x * (V[j].y - V[k].y);
}
area += V[n].x * (V[1].y - V[n-1].y);
return abso(area / 2.0);
}
double distance( Point a, Point b ){
return sqrt( (a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y) ) ;
}
double solve( int n ){
Point p, ptmp, pposible;
int nconvex = 0, x, pos, posa, post;
double area;
memset( vis, 0, sizeof( vis ));
if( n == 1) return 0;
if( n == 2) return distance( Poligono[0], Poligono[1]) * 2.0;
p = Poligono[0];
pos = 0;
for( x = 1; x < n; x++){
if(p.x > Poligono[x].x || (p.x == Poligono[x].x && p.y > Poligono[x].y)){
p = Poligono[x];
pos = x;
}
}
posa = pos;
while( 1 ){
vis[pos] = 1;
convex[nconvex++] = p;
posa = pos;
for(x = 0; x < n; x++){
if( vis[x] == 0){
pos = x;
break;
}
}
for( x = x + 1; x < n; x++){
if( cross( Poligono[posa],Poligono[x], Poligono[pos]) < 0 ){
pos = x;
}else if(cross( Poligono[posa],Poligono[x], Poligono[pos]) == 0 && distance( Poligono[posa] , Poligono[ pos ])
< distance( Poligono[posa] , Poligono[ x ])){
pos = x;
}
}
p = Poligono[ pos ];
if( vis[ pos ] == 1) break;
}
perimetro = 0.0;
convex[ nconvex] = convex[ 0 ];
for( x = 0; x < nconvex; x++) perimetro += distance( convex[ x ], convex[ (x + 1) % nconvex]);
area = area2D_Polygon( nconvex, convex);
printf("%.2lf %.2lf %.2lf\n", perimetro, area, valumen / area);
}
main(){
int x;
while( scanf("%d %lf", &n, &valumen) != EOF && ( n != 0 || valumen != 0 )){
for( x = 0; x < n; x++) scanf("%d %d", &Poligono[ x ].x, &Poligono[ x ].y);
solve( n );
}
return 0;
}
Cualquier sugerencia, explicacion mas detallada, favor de enviarme un correo a rodrigo.burgos@gmail.com